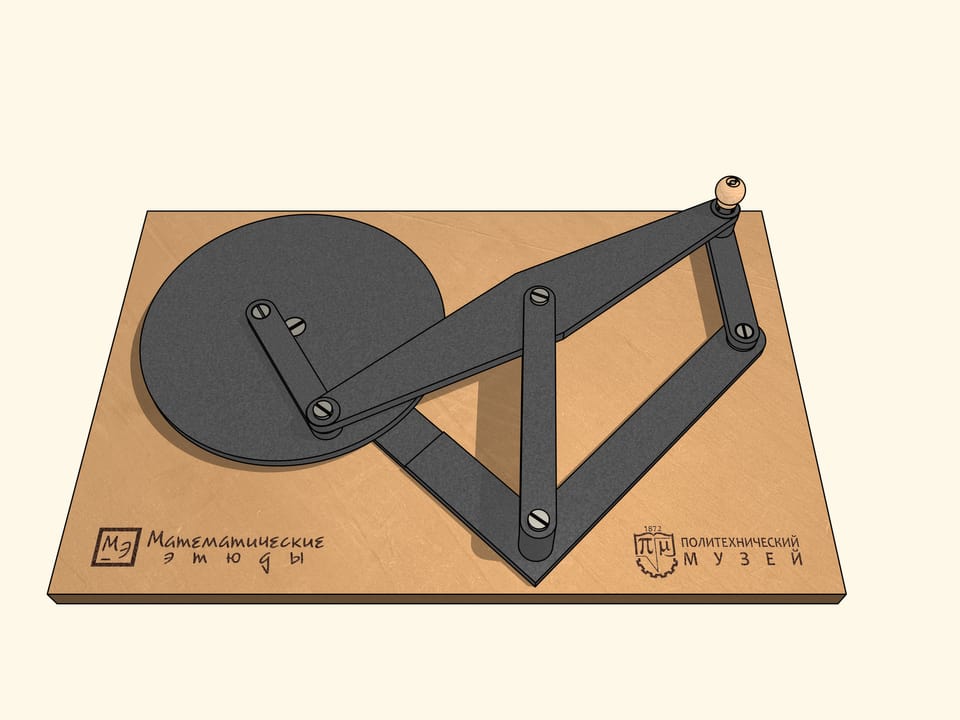
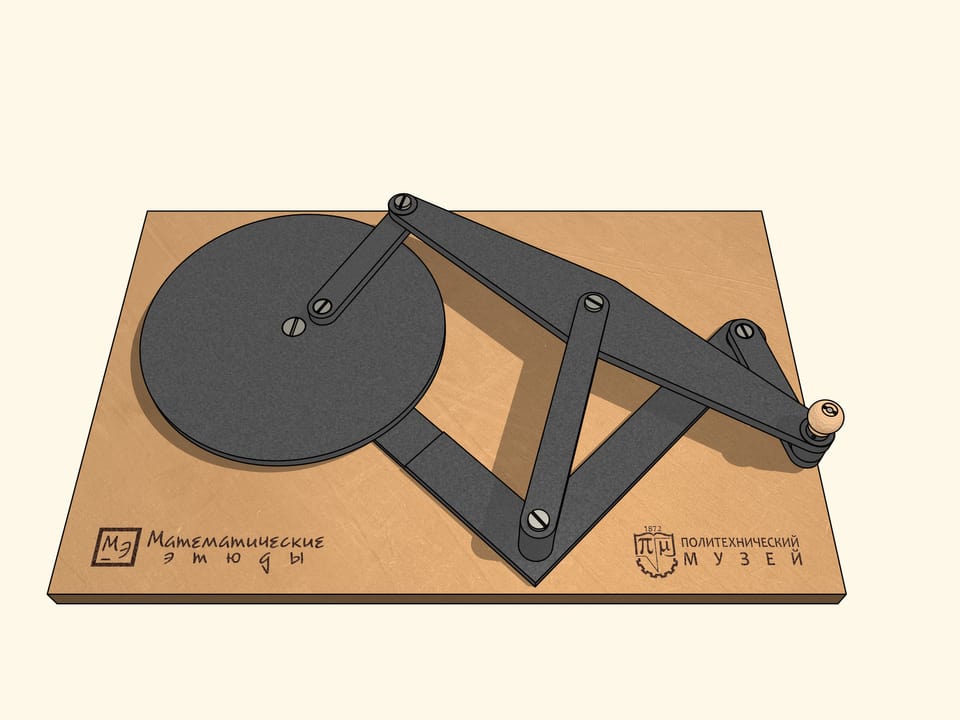
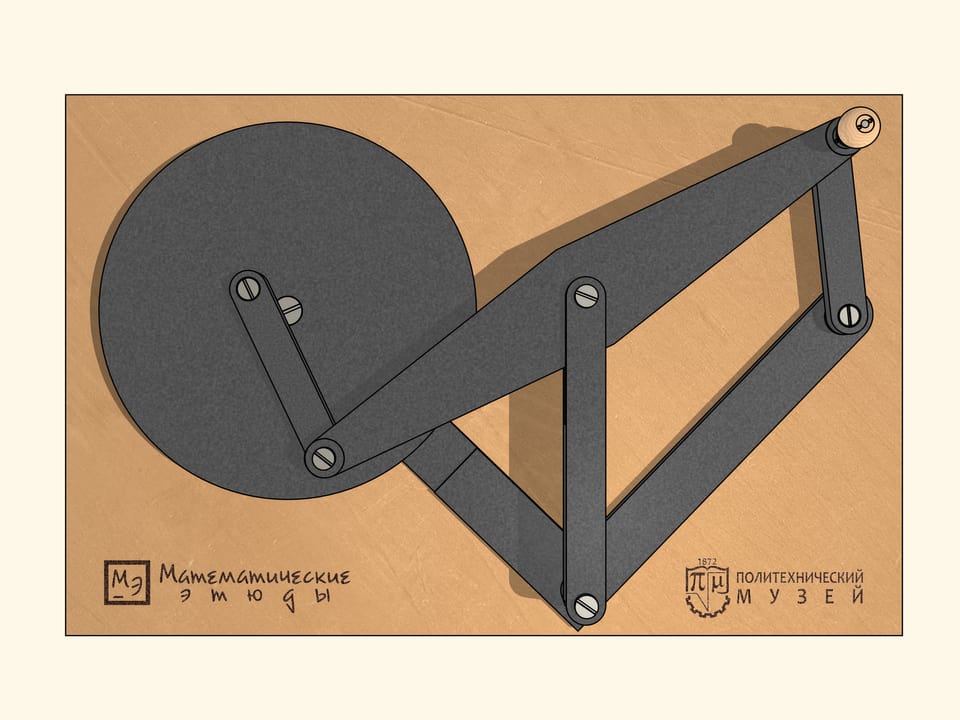
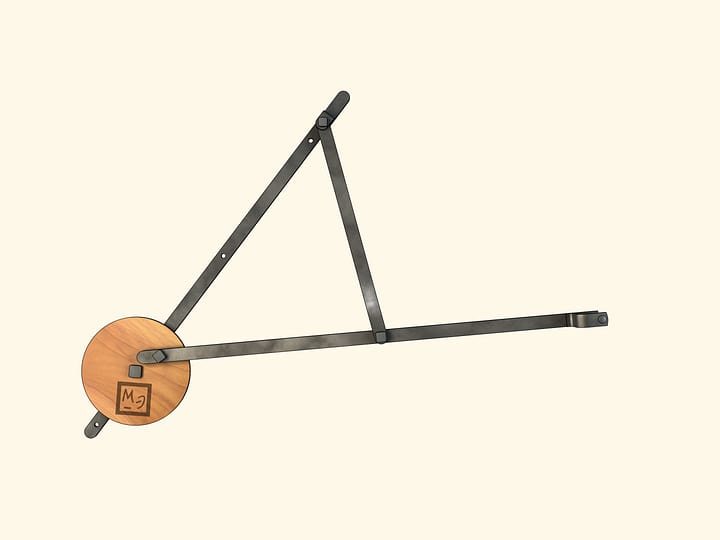
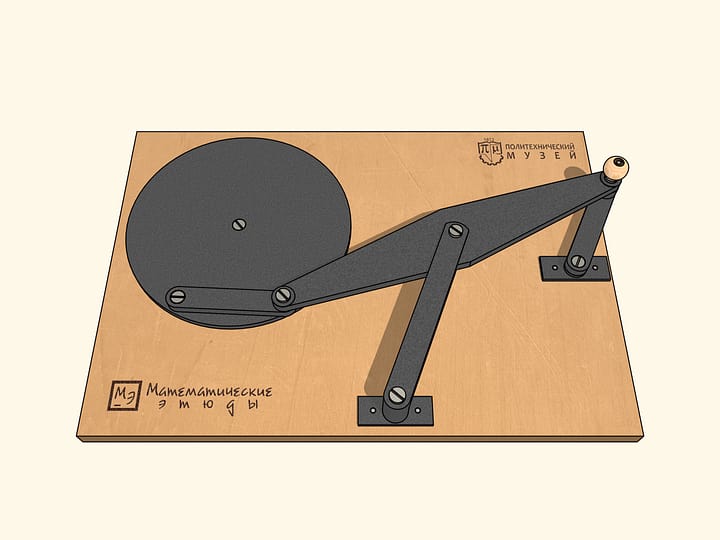
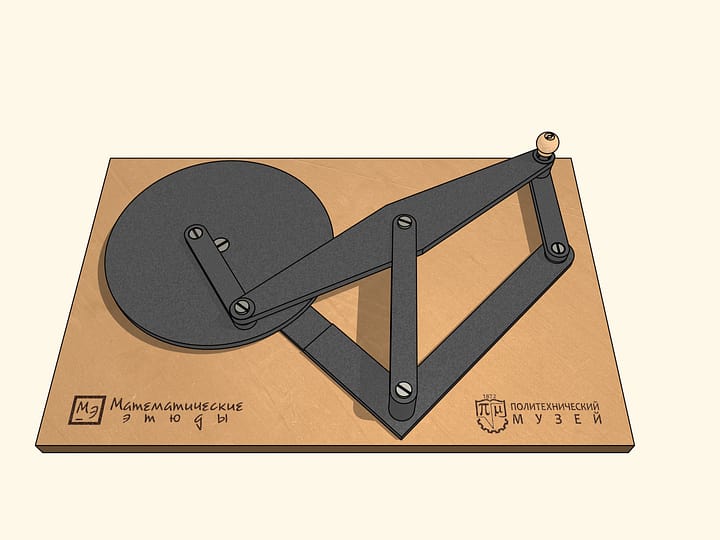
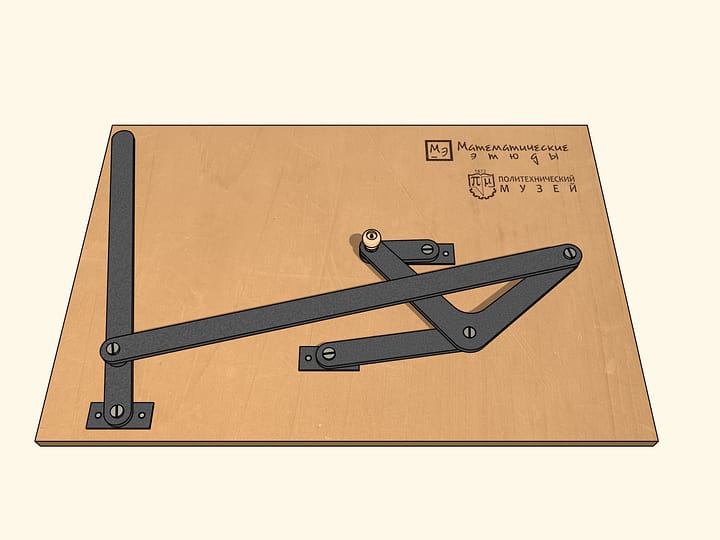
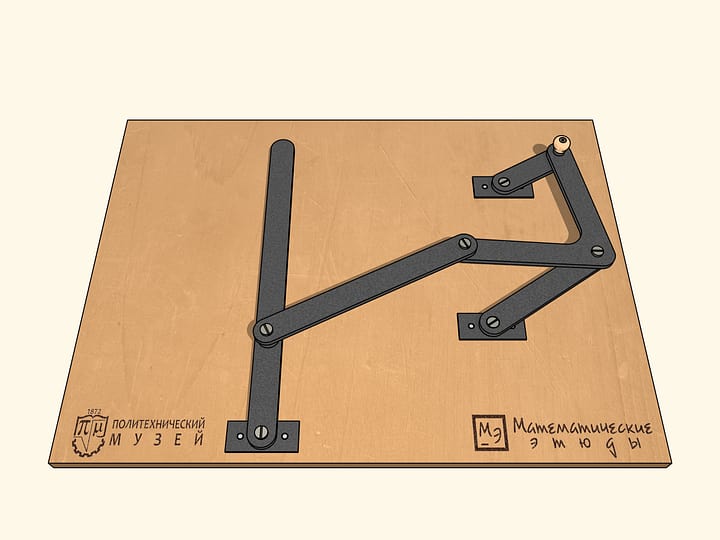
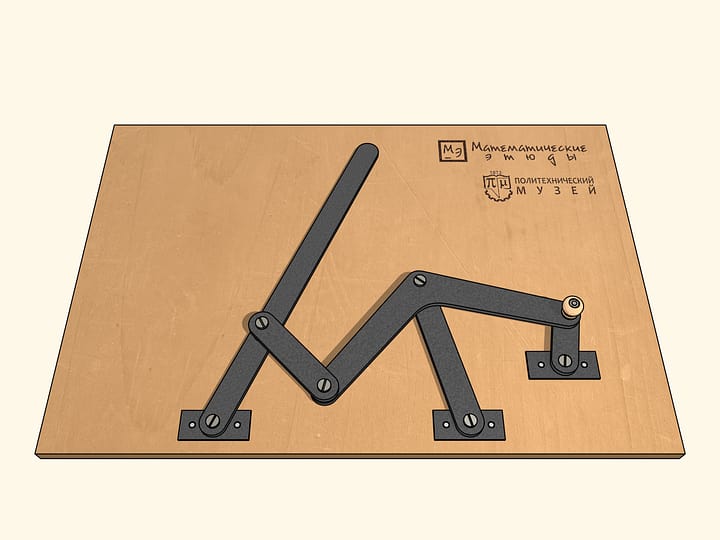
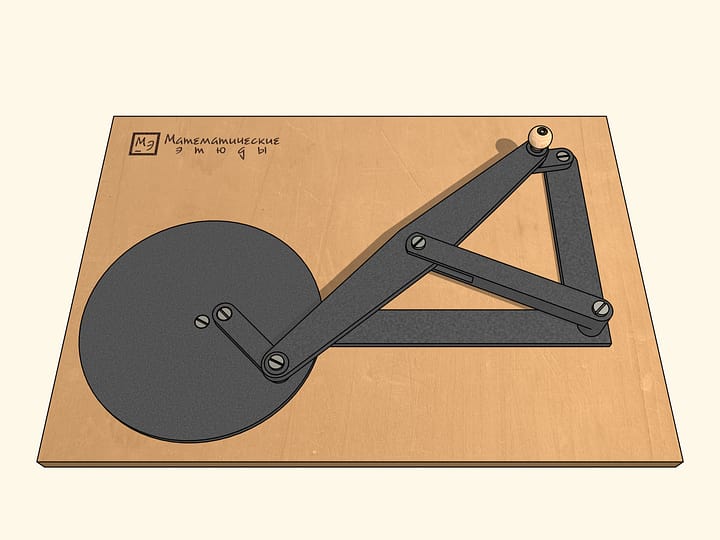
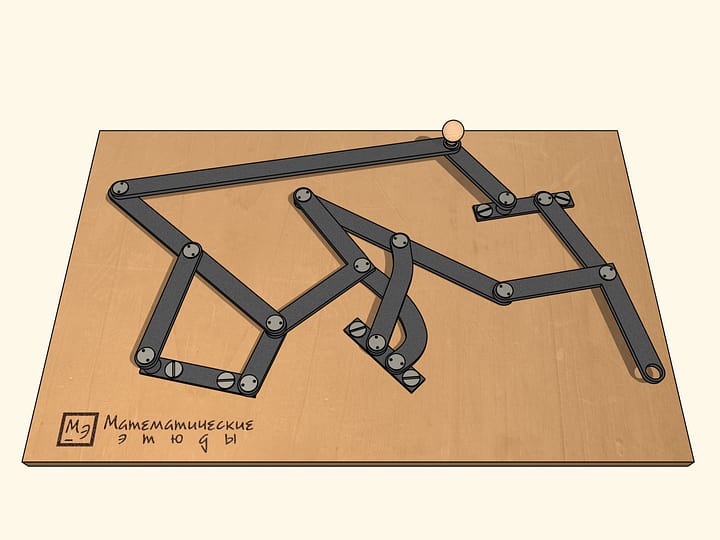
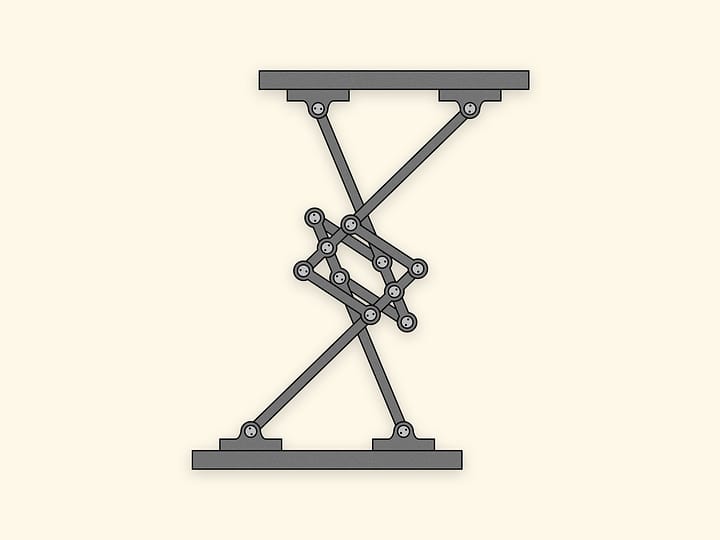
Если раскрутить маховик так же, как и ведущее звено, по часовой стрелке, то за один оборот ведущего звена маховик сделает два оборота. А если же придать маховику движение против часовой стрелки, то за один оборот ведущего звена по часовой стрелке маховик сделает четыре оборота.
Музеи и архивы
Механизм хранится в Политехническом музее (г. Москва); фондохранилище, ПМ № 19461.
Механизм хранится в Musée des arts et métiers du Conservatoire national des arts et métiers (Париж, Франция); CNAM № 11472-0007.
Механизм хранится в Музее истории физики и математики Санкт-Петербургского университета.
Оригинальные статьи П. Л. Чебышева
О простейшей суставочной системе, доставляющей движения, симметричные около оси / По кн.: Полное собрание сочинений П. Л. Чебышева. Том IV. Теория механизмов. — М.—Л.: Изд-во АН СССР. 1948. С. 167–211.
Исследования
И. И. Артоболевский, Н. И. Левитский. Механизмы П. Л. Чебышева / В кн.: Научное наследие П. Л. Чебышева. Вып. II. Теория механизмов. — М.—Л.: Изд-во АН СССР. 1945. С. 30–32.
И. И. Артоболевский, Н. И. Левитский. Модели механизмов П. Л. Чебышева / В кн.: Полное собрание сочинений П. Л. Чебышева. Том IV. Теория механизмов. — М.—Л.: Изд-во АН СССР. 1948. С. 215–217.
Другие материалы
Двигатели, изобретённые академиком Чебышевым // Всемирная иллюстрация. 1893. № 1275. С. 17.
Описание
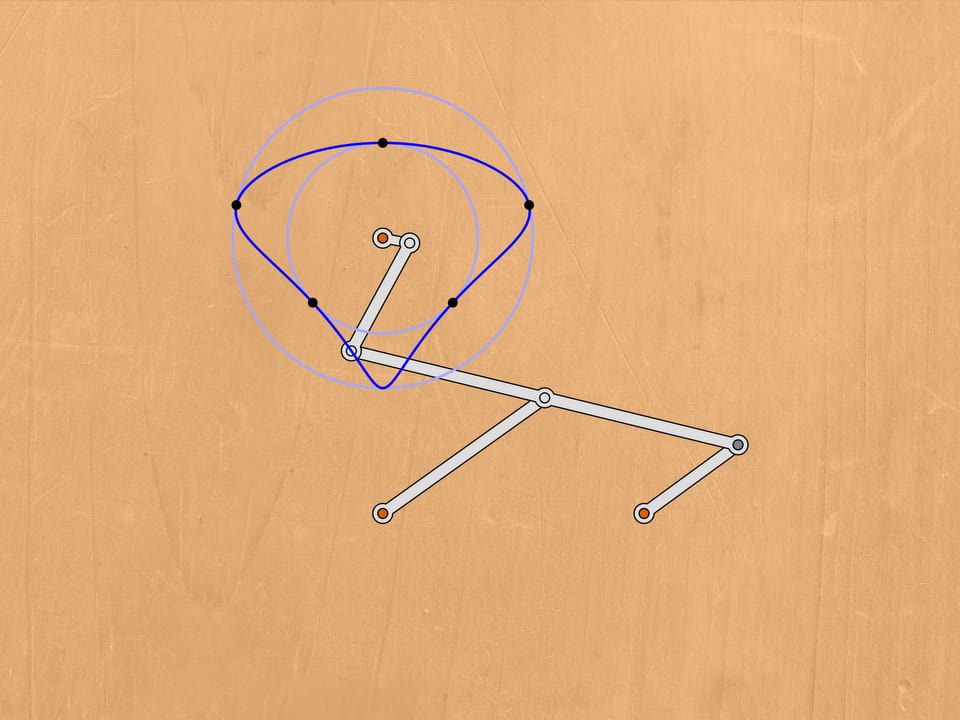
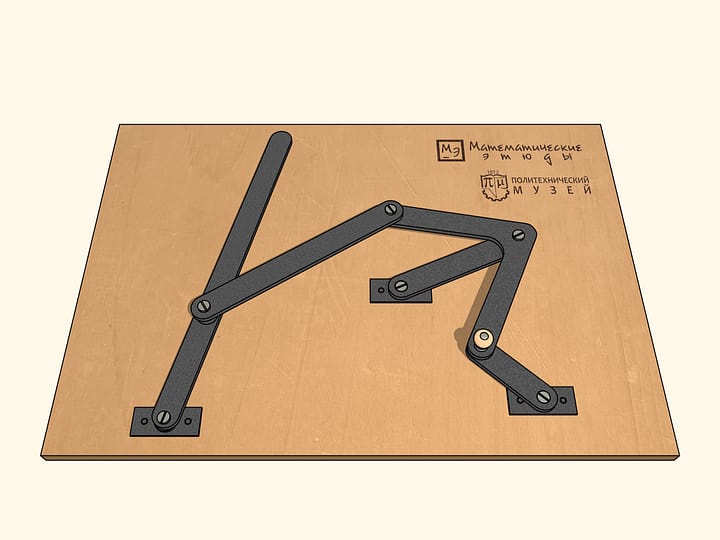
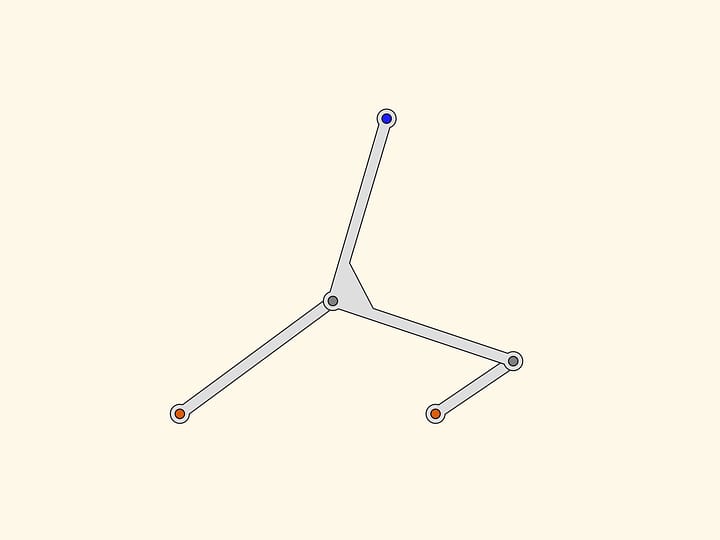
Какое преобразование кривых может выполнять представленное сочленение с одним неподвижным красным шарниром?
Пусть серый шарнир скользит по кривой, симметричной относительно прямой, проходящей через закреплённый красный шарнир. Можно показать, что в таком случае траектория синего шарнира будет также симметрична относительно некоторой прямой, проходящей через неподвижный шарнир. Российский математик Пафнутий Львович Чебышев исследовал вопрос, какова же может быть эта траектория.
Важным частным случаем серой траектории является окружность. На практике он реализуется добавлением одного неподвижного (красного) шарнира и ведущего звена некоторой длины.
Для синей же траектории двумя важными случаями является схожесть её либо с отрезком прямой, либо с окружностью или её дугой. Чебышев пишет: «Здесь мы займёмся рассмотрением случаев, наиболее простых и наичаще представляющихся на практике, а именно когда имеется в виду получить движение по кривой, которой некоторая часть, более или менее значительная, мало разнится от дуги круга или от прямой линии».
Именно к выявлению наилучших параметров этого механизма, решающего перечисленные задачи, Пафнутий Львович впервые сам применяет теорию приближения функций, разработанную им незадолго до этого при изучении параллелограмма Уатта.
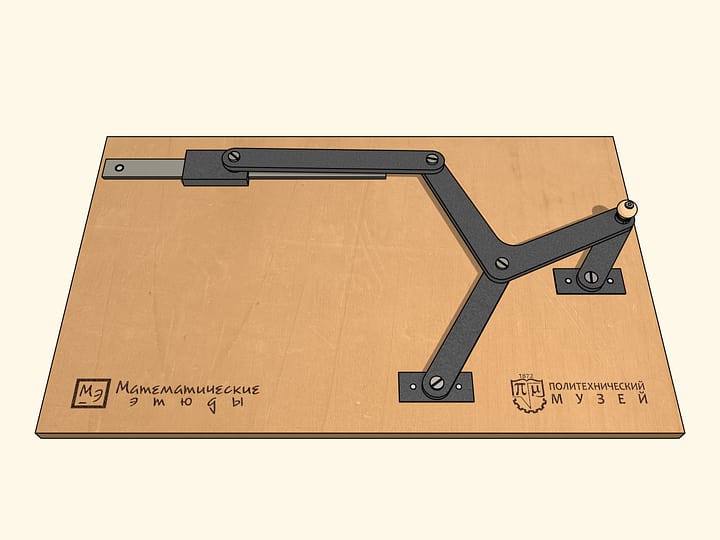
Подбирая параметры лямбда-механизма, Пафнутий Львович Чебышев добивается того, что шатунная кривая поочерёдно касается двух концентрических окружностей, оставаясь всё время между ними.
Достроим лябмда-механизм, добавив неподвижный шарнир и два звена, сумма длин которых равна радиусу большей окружности, а разность — радиусу меньшей.
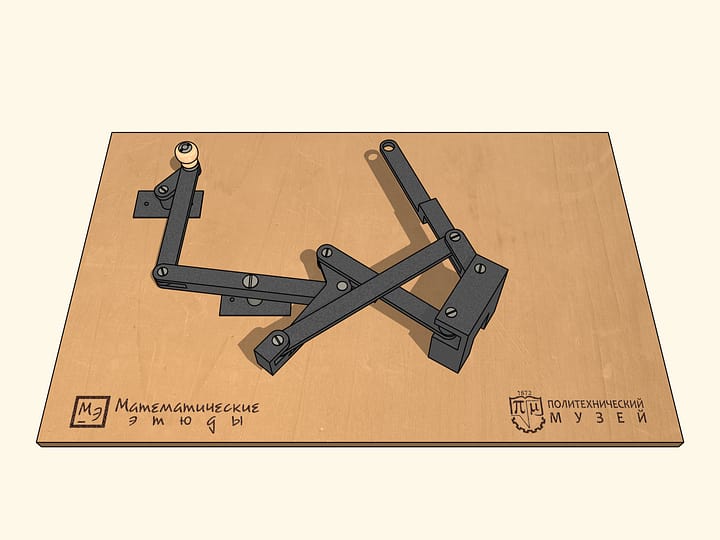
Получившееся устройство имеет точки бифуркации или, как ещё говорят, сингулярные или особые точки. Находясь в такой точке, при одном и том же движении лямбда-механизма по часовой стрелке добавленные звенья могут начать вращаться либо по часовой стрелке, либо против. Таких точек бифуркации в нашем механизме шесть — когда добавленные звенья находятся на одной прямой.
Существует большое и важное направление в математике — теория особенностей — исследование предмета через изучение его особых точек. Очень простым частным случаем является изучение поведения функции через исследование точек её максимума и минимума.
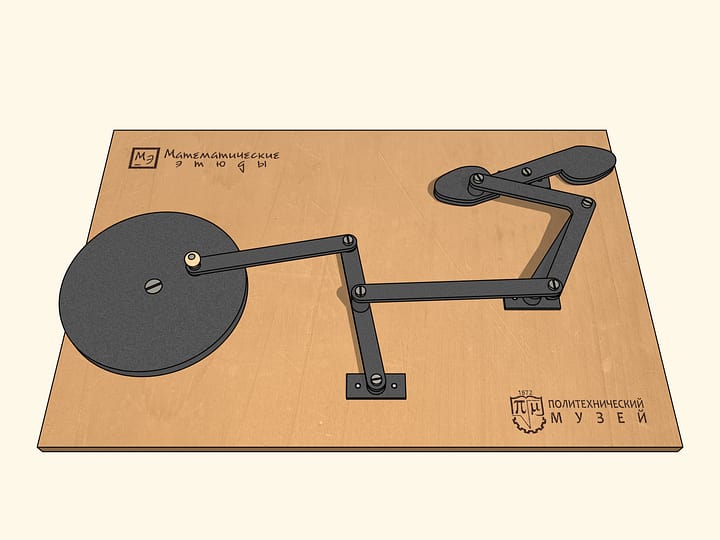
Чтобы наш механизм проходил все шесть особых точек в одном наперёд выбранном направлении, маленькое звено связывают с маховиком, которое будучи раскрученным в какую-то сторону, выводит механизм из особой точки вращающимся в ту же сторону.
Если из точки бифуркации раскрутить маховик так же, как и ведущее звено, по часовой стрелке, то за один оборот ведущего звена маховик сделает два оборота.
Если же из особой точки придать маховику движение против часовой стрелки, то за один оборот ведущего звена по часовой стрелке маховик сделает целых четыре оборота!
В этом и заключается парадоксальность этого механизма, придуманного и сделанного Пафнутием Львовичем Чебышевым. Казалось бы, плоский шарнирный механизм должен работать однозначно, однако, как видим, это не всегда так. И причиной являются особые точки.
Модель механизма
Геометрическая модель, созданная проектом «Математические этюды».